En 1854 George Boole publico una obra titulada “investigación de las leyes del pensamiento, sobre las que se basan las teorías matemáticas de la lógica y la probabilidad”. En esta publicación formulo la idea del algebra de operaciones lógicas que se conoce hoy en día como Algebra de Boole. El algebra de Boole es una forma que permite expresar y analizar operaciones de circuitos lógicos.
Operaciones Booleanas
En el algebra de Boole, una variable es un símbolo que se utiliza para representar magnitudes lógicas. Cualquier variable puede tener un valor de 1 o 0. El complemento es el inverso de la variable. Un literal se define como una variable o su complemento.
Adición Booleana
La adición Booleana es equivalente a la operación lógica OR. En algebra de Boole, un termino suma es una suma de literales. En circuitos lógicos, un termino suma se produce mediante la operación lógica OR de dos literales. El resultado de la suma es 1 cuando uno o más de los literales es uno.
Las reglas de la suma son:
| Entradas | Salida | |
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Multiplicación Booleana
La multiplicación Booleana es equivalente a la operación lógica AND. En algebra de Boole, un termino producto es una producto de literales. En circuitos lógicos, un término producto se produce mediante la operación lógica AND de dos literales. El resultado de la multiplicación es 1 cuando todos sus literales son uno.
Las reglas de la multiplicación son:
| Entradas | Salida | |
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Leyes del Algebra de Boole
Al igual que en otras áreas de las matemáticas, existe en el algebra de Boole una serie de leyes que resuelven determinados problemas en las implementaciones de circuitos lógicos.
Ley Commutativa
La ley conmutativa indica que el orden de las variables no altera el resultado. Entonces la ley conmutativa para la adición de dos variables se describe como:
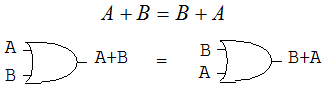
La ley conmutativa para la multiplicación de dos variables se describe como:
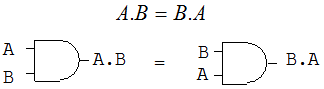
Ley Asociativa
La ley asociativa para la adición de tres variables se describe como:
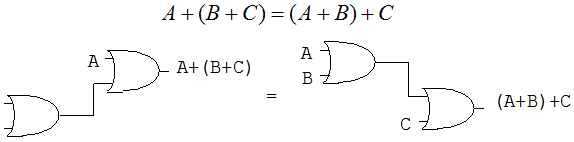
La ley asociativa para la multiplicación de dos variables se describe como:
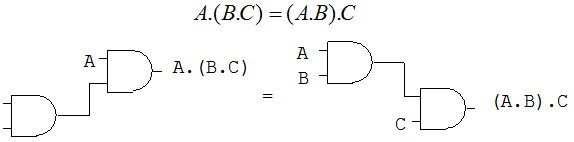
Ley Distributiva
La ley distributiva para tres variables se describe como:
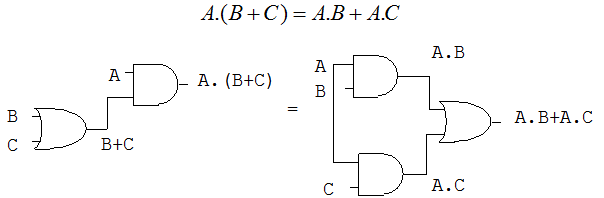
Reglas del Algebra de Boole
Existen unas reglas básicas para la manipulación y simplificación de expresiones Booleanas. Estas reglas se describen en la siguiente tabla.
| Nº | REGLA | DESCRIPCION |
| 1 | 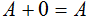 | Al aplicar la operación OR a una variable y a cero el resultado es el valor de la variable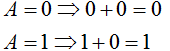 |
| 2 | 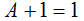 | Al aplicar la operación OR a una variable y a uno el resultado es uno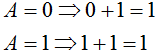 |
| 3 | 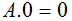 | Al aplicar la operación AND a una variable y a cero el resultado es cero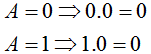 |
| 4 | 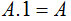 | Al aplicar la operación AND a una variable y a uno el resultado es el valor de la variable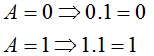 |
| 5 | 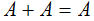 | Al aplicar la operación OR a una variable consigo misma el resultado es el valor de la variable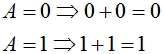 |
| 6 | 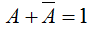 | Al aplicar la operación OR a una variable con su complemento el resultado es 1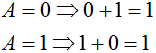 |
| 7 | 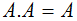 | Al aplicar la operación AND a una variable consigo misma el resultado es el valor de la variable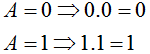 |
| 8 | 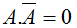 | Al aplicar la operación AND a una variable con su complemento el resultado es 0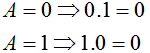 |
| 9 | 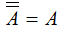 | El doble complemento de una variable es igual a la variable |
| 10 | 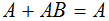 | Aplicando la ley distributiva y las reglas 2 y 4 de esta tabla se puede deducir esta regla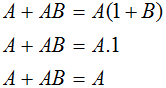 |
| 11 | 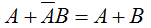 | Aplicando varias reglas de esta tabla se puede deducir esta regla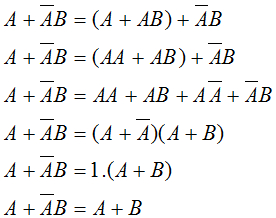 |
| 12 | 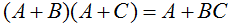 | Aplicando varias reglas de esta tabla se puede deducir esta regla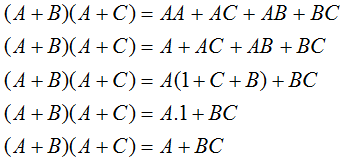 |
Teoremas de DeMorgan
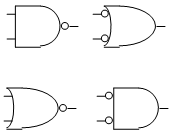
DeMorgan, fue un matemático que estuvo relacionado con Boole. Propuso dos teoremas que están fuertemente relacionados con el algebra de Boole. Los teoremas de DeMorgan, demuestran las equivalencias entre las compuertas NAND y Negativa OR y las compuertas NOR y Negativa AND.
El primer teorema de DeMorgan se enuncia como: El complemento de un producto de variables es igual a la suma de los complementos de las variables.
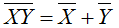
El segundo teorema de DeMorgan se enuncia como: El complemento de una suma de variables es igual al producto de los complementos de las variables.
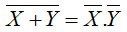
Sus compuertas equivalentes son:
No hay comentarios:
Publicar un comentario