En cualquier lenguaje de programación es posible construir estructuras que almacenen conjuntos de datos. Estas estructuras pueden tener una o más dimensiones. Las estructuras con una dimensión se denominan arreglos y las estructuras con dos dimensiones se denominan matrices. Hay casos particulares en que se requiere el uso de más de dos dimensiones, en ese caso se denominan arreglos multidimensionales. Java además incluye en su API clases que proveen servicios para el almacenamiento de objetos denominadas colecciones.
Arreglos
Un arreglo es una estructura que posee un conjunto de datos del mismo tipo. Los arreglos en Java son objetos pero sus elementos pueden ser tipos primitivos de datos o clases. Un arreglo tiene las siguientes características:
- Nombre. El nombre identifica al arreglo y a través de este, se accede al arreglo para su lectura y escritura de información. La identificacion del arreglo con el nombre, se realiza mediante la declaracion del arreglo
int [] miArreglo;
miArreglo = new int[20]
int [] miArreglo = new int[20]
miArreglo[0]=10;
String dias[] = {"lunes", "martes", "miercoles", "jueves", "viernes", "sabado", "domingo"};
Calculo de promedio en un arreglo
Para calcular el promedio en un arreglo, basta con hacer la sumatoria de números del arreglo y dividir en el número de elementos
Su implementación es la siguiente
import java.util.Scanner;
public class EjemplosArreglos {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
double promedio;
double sumatoria=0;
int tamano=10;
double []arreglo = new double[tamano];
for(int i=0; i<tamano; i++){
arreglo[i]=s.nextInt();
}
System.out.println("El arreglo original es:");
for(int i=0; i<tamano; i++){
System.out.println(arreglo[i]);
}
for(int i=0; i<tamano; i++){
sumatoria+=arreglo[i];
}
promedio=sumatoria/tamano;
System.out.println("El promedio es:"+promedio);
}
}
Para probar el algoritmo, se usan los sigientes datos
25 34 12 8 7 11 45 20 21 10
El arreglo original es: 25.0 34.0 12.0 8.0 7.0 11.0 45.0 20.0 21.0 10.0 El promedio es:19.3
Búsqueda lineal
La búsqueda lineal en un arreglo, consiste en la implementación de un proceso iterativo que recorre todo el arreglo. Se debe contar con un índice que inicia en 0 e incrementa en cada iteración. En cada iteración consulta a través de un “if” si el valor a buscar es igual al valor del arreglo en índice actual. En caso de ser verdadero, debe retornar el índice. Si se compara todo el arreglo y en ningún caso encuentra el valor, retorna el valor -1. Su implementación es la siguiente
public class EjemplosArreglos {
public static void main(String[] args) {
int []numeros = new int[10];
for(int i=0;i<numeros.length;i++){
numeros[i]=i*5;
}
System.out.println("El arreglo original es:");
for(int i=0;i<numeros.length;i++){
System.out.println(numeros[i]);
}
EjemplosArreglos ejemplo = new EjemplosArreglos();
int indice=ejemplo.busquedaLineal(numeros, 40);
System.out.println("El indice del valor '40' es: "+indice);
}
public int busquedaLineal(int []arreglo, int clave){
for(int i=0;i<arreglo.length;i++){
if(arreglo[i]==clave){
return i;
}
}
return -1;
}
}
Al ejecutar el algoritmo, el resultado es el siguiente.
El arreglo original es: 0 5 10 15 20 25 30 35 40 45 El indice del valor '40' es: 8
Búsqueda binaria
La búsqueda binaria en un arreglo es más eficiente y sofisticada que la búsqueda lineal y consiste en la implementación de un proceso recursivo que recibe el arreglo y el valor que se desea buscar. Esta búsqueda debe realizarse con arreglos ordenados. Se inicia consultando el valor ubicado en la mitad del arreglo. Si el valor a buscar es igual, se retorna el índice. Si el valor a buscar es menor, se hace el llamado recursivo realizando la búsqueda con los valores desde la posición inicial hasta la posición anterior a la mitad, pero si no hay elementos entre estas posiciones, retorna -1. Si el valor a buscar es mayor, se hace el llamado recursivo realizando la búsqueda con los valores desde la posición siguiente a la mitad hasta la última posición, pero si no hay elementos entre estas posiciones, retorna -1.
Este algoritmo se puede implementar sin usar recursividad, sin embargo, es recomendable implementarlo de esta forma para optimizar el código. Su implementación es la siguiente
public class EjemplosArreglos {
public static void main(String[] args) {
int []numeros = new int[10];
for(int i=0;i<numeros.length;i++){
numeros[i]=i*5;
}
System.out.println("El arreglo original es:");
for(int i=0;i<numeros.length;i++){
System.out.println(numeros[i]);
}
EjemplosArreglos ejemplo = new EjemplosArreglos();
int indice=ejemplo.busquedaBinaria(numeros, 40, 0, numeros.length-1);
System.out.println("El indice del valor '40' es: "+indice);
}
public int busquedaBinaria(int []arreglo, int clave, int posInicial, int posFinal){
int posMitad=(posFinal+posInicial)/2;
if(clave==arreglo[posMitad]){
return posMitad;
}else if(clave<arreglo[posMitad]){
if(posMitad-1<=posInicial){
return -1;
}else{
return busquedaBinaria(arreglo,clave,posInicial,posMitad-1);
}
}else{
if(posMitad+1>=posFinal){
return -1;
}else{
return busquedaBinaria(arreglo,clave,posMitad+1,posFinal);
}
}
}
}
El arreglo original es: 0 5 10 15 20 25 30 35 40 45 El indice del valor '40' es: 8
Ordenamiento de un arreglo de números
Considerando un arreglo tipo int, es posible ordenarlo utilizando diferentes técnicas que varían en su complejidad de implementación y de ejecución. La técnica más simple es el ordenamiento de burbuja.
El algoritmo de burbuja consiste en evaluar cada elemento por los demás elementos. Para ello, se requiere un índice que recorra el arreglo desde la primera posición hasta la penúltima. Adicionalmente se requiere un índice que recorra el arreglo desde la siguiente posición del primer índice hasta la última posición del arreglo. Con base en un arreglo denominado A de 5 posiciones y los datos en cada posición son: 8, 3, 5, 9, 1, la representación del ordenamiento mediante el algoritmo de burbuja se presenta en la siguiente figura.

Su implementación es la siguiente
import java.util.Scanner;
public class EjemplosArreglos {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int []arreglo = new int[10];
int indice=0;
while(indice<10){
arreglo[indice]=s.nextInt();
indice++;
}
System.out.println("El arreglo original es:");
for(int i=0; i<indice; i++){
System.out.println(arreglo[i]);
}
for(int i=0; i<indice-1; i++){
for(int j=i+1; j<indice; j++){
if(arreglo[i]>arreglo[j]){
int temporal=arreglo[i];
arreglo[i]=arreglo[j];
arreglo[j]=temporal;
}
}
}
System.out.println("El arreglo ordenado es:");
for(int i=0; i<indice; i++){
System.out.println(arreglo[i]);
}
}
}
25 34 12 8 7 9 45 20 21 10
El arreglo original es: 25 34 12 8 7 9 45 20 21 10 El arreglo ordenado es: 7 8 9 10 12 20 21 25 34 45
Matrices
Una matriz es un arreglo bidimensional. Una matriz cuenta con filas y columnas. Con base en la combinación de fila y columna, se puede acceder a cada uno de los elementos de la matriz.
Una matriz tiene las siguientes características:
- Nombre. El nombre identifica al arreglo y a través de este, se accede al arreglo para su lectura y escritura de información. La identificación de la matriz con el nombre, se realiza mediante la declaración de la matriz
int [][] miMatriz;
miMatriz = new int[3][4];
int [][] miMatriz = new int[3][4];
int [][] miMatriz ={{1,2,3,4},{5,6,7,8},{9,10,11,12}
La siguiente figura representa una matriz en Java

Calculo de la traspuesta de una matriz
La traspuesta de una matriz consiste en intercambiar filas por columnas y viceversa. Su implementación es la siguiente
public class EjemplosMatrices {
public static void main(String[] args) {
int [][] miMatriz ={{1,2,3},
{4,5,6},
{7,8,9}
};
int [][] miMatrizTraspuesta = new int[3][3];
System.out.println("La matriz original es:");
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
System.out.print(miMatriz[i][j]+"\t");
}
System.out.println();
}
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
miMatrizTraspuesta[j][i]=miMatriz[i][j];
}
}
System.out.println("La matriz traspuesta es:");
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
System.out.print(miMatrizTraspuesta[i][j]+"\t");
}
System.out.println();
}
}
}
La matriz original es: 1 2 3 4 5 6 7 8 9 La matriz traspuesta es: 1 4 7 2 5 8 3 6 9
Multiplicación de matrices
Dadas dos matrices A y B donde el número de columnas de la matriz A es igual al número de filas de la matriz B que se denota como:
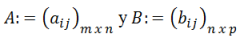
La multiplicación de A x B se denota como:
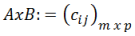
Donde cada elemento cij se calcula mediante:
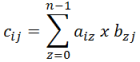
Para dos matrices 3 x 3, la representación grafica de la multiplicación se presenta en la siguiente figura
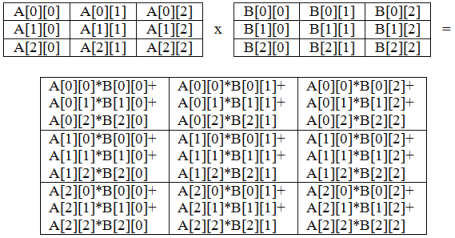
La implementación para dos matrices de 3 x 3 es la siguiente
public class EjemplosMatrices {
public static void main(String[] args) {
int [][] A ={{1,2,3},
{4,5,6},
{7,8,9}
};
int [][] B ={{9,8,7},
{6,5,4},
{3,2,1}
};
int [][] C = new int[3][3];
System.out.println("La matriz A es:");
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
System.out.print(A[i][j]+"\t");
}
System.out.println();
}
System.out.println("La matriz B es:");
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
System.out.print(B[i][j]+"\t");
}
System.out.println();
}
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
for(int k=0; k<3; k++){
C[i][j]+=A[i][k]*B[k][j];
}
}
}
System.out.println("La multiplicacion es:");
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
System.out.print(C[i][j]+"\t");
}
System.out.println();
}
}
}
La matriz A es: 1 2 3 4 5 6 7 8 9 La matriz B es: 9 8 7 6 5 4 3 2 1 La multiplicacion es: 30 24 18 84 69 54 138 114 90
Profesor en que caso se necesitaria declarar una matriz de 3 dimensiones o mas, y si existe un caso de estos, como se podria implementar en un programa, podria colocar un ejemplo en este blog?.
ResponderEliminarMUCHAS GRACIAS POR SU RESPUESTA.
Precisamente hice hice un juego de sudoku en donde tuve que crear una matriz de 3 dimensiones.
EliminarLa sintaxis para ello es:
int [][][]matriz = new int [3][3][4];
La intencion de esta matriz es colocar numeros de ayuda en el juego de sudoku. Entonces, el sudoku tiene 3 cuadrantes, cada cuadrante tiene 3 filas (el primer indice de la matriz) y tres columnas (el segundo indice de la matriz) y cada celda tiene 4 numeros de ayuda (el tercer indice de la matriz).